Like us!

Have a Look!

WhatsApp Message

Share Link

Trigonometric ratios of Complementary Angles

Introduction to Trigonometry II - Concepts

Trigonometric ratios of Complementary Angles

Trigonometric Identity Involving Sine And Cosine

Trigonometric Identity Involving Secant And Tangent

Trigonometric Identity Involving Cosecant And Cotangent

Trigonometric Identities

Class - 10th CBSE Subjects

Concept Explanation

Trigonometric ratios of Complementary Angles

Trigonometric ratios of Complementary Angles:

Recall that two angles are said to be complementary if their sum equals $90^{circ}$ . In $Delta ABC$ , right - angled at B, do you see any pair of complementary angles?

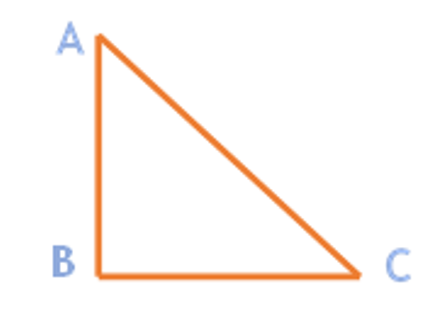
Since $angle A+angle C=90^{circ},$ they form such a pair, we have:

$sin A=frac{BC}{AC}$ $cos A=frac{AB}{AC}$ $tan A=frac{BC}{AB}$

$cosec A=frac{AC}{BC}$ $sec A=frac{AC}{AB}$ $cot A=frac{AB}{BC}$ (1)

Now let us write the trigonometric ratios for $angle C=90^{circ}-angle A$ .

For convenience, we shall write $90^{circ}-A$ instead of $90^{circ}-angle A$ .

What would be the side opposite and the side adjacent to the angle $90^{circ}- A?$

You will find that AB is the side opposite and BC is the side adjacent to the angle $90^{circ}- A$ . Therefore,

$sin(90^{circ}-A)=frac{AB}{AC}$ $cos(90^{circ}-A)=frac{BC}{AC}$ $tan(90^{circ}-A)=frac{AB}{BC}$

$cosec(90^{circ}-A)=frac{AC}{AB}$ $sec(90^{circ}-A)=frac{AC}{BC}$ $cot(90^{circ}-A)=frac{BC}{AB}$ ....... (2)

Now, compare the ratios in (1) and (2) , observe that :

$sin(90^{circ}-A)=frac{AB}{AC}=cos A;;and;;cos(90^{circ}-A)=frac{BC}{AC}=sin A$

Also, $tan(90^{circ}-A)=frac{AB}{BC}=cot ;A;;and;;cot;(90^{circ}-A)=frac{BC}{AB}=tan ;A$

$sec;(90^{circ}-A)=frac{AB}{BC}=cosec ;A;;and;;cosec;(90^{circ}-A)=frac{AC}{AB}=sec; A$

So, $sin;(90^{circ}-A)=cos; A$ , $cos;(90^{circ}-A)=sin; A$ ,

$tan;(90^{circ}-A)=cot ;A$ , $cot;(90^{circ}-A)=tan; A$

$sec;(90^{circ}-A)=cosec ;A$ $cosec;(90^{circ}-A)=sec ;A$

for all values of angle A lying between $0^{circ}$ and $90^{circ}$ . check whether this holds for $A=0^{circ}$ or $A=90^{circ}$ .

Example 1: Evaluate $frac{tan; 65^{circ}}{cot; 25^{circ}}$

Solution: We know: $cot ;A = tan; (90^{circ}-A)$

So, $cot; 25^{circ} = tan ;(90^{circ}-25^{circ})=tan;65^{circ}$

i.e, $frac{tan;65^{circ}}{cot;25^{circ}}-=frac{tan;65^{circ}}{tan;65^{circ}}=1$

Sample Questions

(More Questions for each concept available in Login)

Question : 1

Find the value of $If; sin; 58^0= frac{m}{n}. Find ; the;value ;of;sin;32^0$
A. $frac{n}{m}$	B. $frac{m}{n}$	C. m	D. n
Right Option : B
View Explanation

Question : 2

$frac{sin;18^0}{cos; 72^0}$ =______________________
A. 0	B. 1	C. $frac{1}{2}$	D. Not Defined
Right Option : B
View Explanation

Question : 3

$sin;35^0.; sin;55^0 - cos ;35^0.; cos;55^0$ = ___________________
A. 0	B. $frac{1}{3}$	C. 2	D. $frac{1}{4}$
Right Option : A
View Explanation

Chapters

Polynomial I

Polynomials II

Pair of Linear Equations I

Pair of Linear Equations II

Real Numbers I

Real Numbers II

Coordinate Geometry I

Coordinate Geometry II

Quadratic Equations I

Quadratic Equations II

Arithmetic Progression I

Arithmetic Progression II

Introduction to Trigonometry I

Introduction to Trigonometry II

Surface Area and Volume I

Surface Area and Volume II

Areas Related to Circles

Some Applications of Trigonometry

Content / Category

IMO-Mathematics Olympiad

Central Government Service

ISO - Science Olympiads

State Government Services

Banking And Insurance

Railways & Metro Services

MBA Entrance

Law Entrance

English Proficiency

Reasoning Proficiency

Computer Proficiency

Navodaya Entrance 6th & 9th

Sainik School Entrance

Class / Course

Our Areas of Expertise

IMO-Mathematics Olympiad

Central Government Service

ISO - Science Olympiads

State Government Services

Banking And Insurance

Railways & Metro Services

MBA Entrance

Law Entrance

English Proficiency

Reasoning Proficiency

Computer Proficiency

Navodaya Entrance 6th & 9th

Sainik School Entrance

Andhra Bank

Students / Parents Reviews [10]

It was good as the experience because as we had come here we had been improved in a such envirnment created here.Extra is taught which is beneficial for future.

Eshan Arora

8th

A marvelous experience with Abhyas. I am glad to share that my ward has achieved more than enough at the Ambala ABHYAS centre. Years have passed on and more and more he has gained. May the centre f...

Archit Segal

7th

My experience was very good with Abhyas academy. I am studying here from 6th class and I am satisfied by its results in my life. I improved a lot here ahead of school syllabus.

Ayan Ghosh

8th

My experience with Abhyas is very good. I have learnt many things here like vedic maths and reasoning also. Teachers here first take our doubts and then there are assignments to verify our weak poi...

Shivam Rana

7th

About Abhyas metholodology the teachers are very nice and hardworking toward students.The Centre Head Mrs Anu Sethi is also a brilliant teacher.Abhyas has taught me how to overcome problems and has...

Shreya Shrivastava

8th

I have spent a wonderful time in Abhyas academy. It has made my reasoning more apt, English more stronger and Maths an interesting subject for me. It has given me a habbit of self studying

Yatharthi Sharma

10th

Being a parent, I saw my daughter improvement in her studies by seeing a good result in all day to day compititive exam TMO, NSO, IEO etc and as well as studies. I have got a fruitful result from m...

Prisha Gupta

8th

Abhyas is a complete education Institute. Here extreme care is taken by teacher with the help of regular exam. Extra classes also conducted by the institute, if the student is weak.

Om Umang

10th

It was a good experience with Abhyas Academy. I even faced problems in starting but slowly and steadily overcomed. Especially reasoning classes helped me a lot.

Cheshta

10th

Abhyas Methodology is very good. It is based on according to student and each child manages accordingly to its properly. Methodology has improved the abilities of students to shine them in future.

Manish Kumar

10th

View All

Attention !!!!!

Trigonometric ratios of Complementary Angles

Trigonometric ratios of Complementary Angles

Students / Parents Reviews [10]

Eshan Arora

Archit Segal

Ayan Ghosh

Shivam Rana

Shreya Shrivastava

Yatharthi Sharma

Prisha Gupta

Om Umang

Cheshta

Manish Kumar